We know that quantum mechanics are save memory in modelling stochastic processes, but how great can this advantage be and does it scale? In our latest work, we study a family of processes where the memory advantage does indeed scale, and very impressively at that. In particular, as the amount of classical memory required to simulate this family diverges towards infinity, the amount of quantum memory requires stays bounded at some finite value.
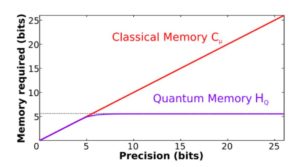
In particular, we demonstrate this for a particularly interesting scenario where we wish to simulate some continuous variable stochastic process to progressively greater and greater precision. The amount of classical memory grows linearly with the amount precision we desire, while perfect simulation would require knowledge of a continuous variable parameter and thus diverge to infinity. Quantum mechanically, this memory remains bounded.
- Unbounded memory advantage in stochastic simulation using quantum mechanics
A. Garner, Q Liu, J Thompson, V Vedral, M Gu, - arXiv preprint arXiv:1609.04408,
